フェーズ概要 参考:IBM
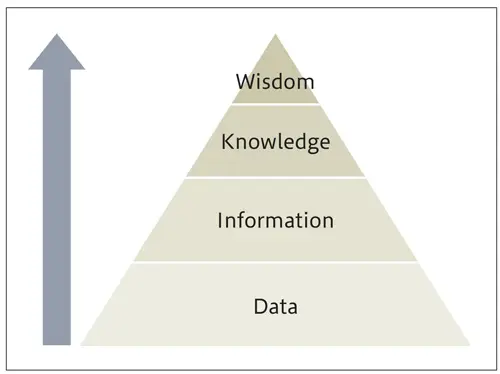
DIKWピラミッド
Wisdom : 判断・解釈・新たな価値
Knowledge : 可視化+背景知識・経験
Information : Dataを構造化
Data : 観測された事実の集まり
定義
偏差 deviation 平均値からの差
標準偏差 standard deviation 平均値からの標準的な差
分散 variance 標準偏差の2乗
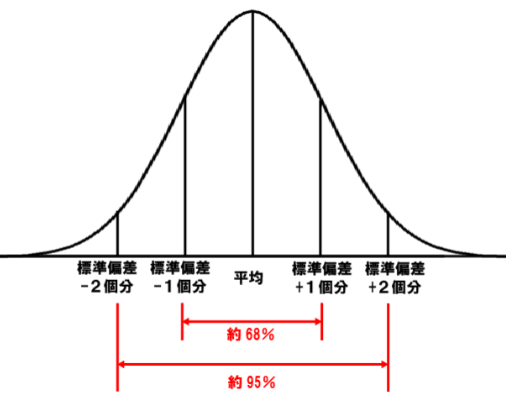
正規分布/ガウス分布 normal distribution/Gaussian distribution
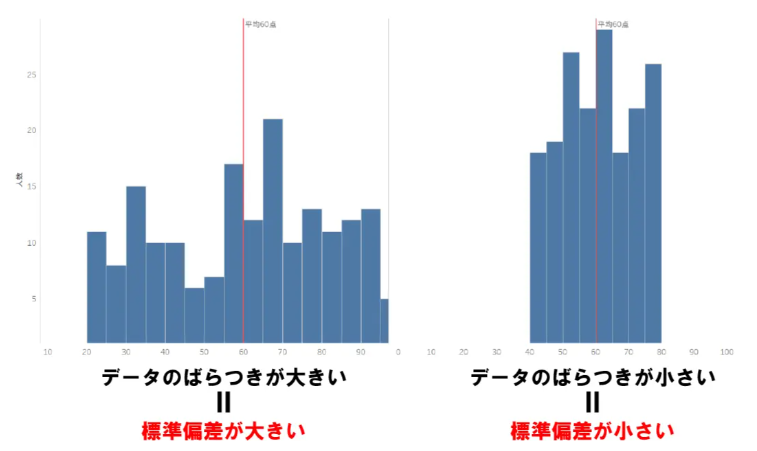
分散 variance 標準偏差stdの2乗
歪度 skewness +0.5以上:左偏 0:正規分布 -0.5以下:右偏
※+0.5~-0.5以内 ≒ 正規分布
尖度 kurtosis 2.5以下:扁平裾太 3:正規分布 3.5以上:尖り裾細
※2.5~3.5範囲内 ≒ 正規分布
# 平均/標準偏差/最小/最大/四分位点/分散/歪度/尖度
col = "カラム名"
print(df[col].describe())
print(f'分散 variance : {df[col].var():.1f} ※標準偏差stdの2乗')
print(f'歪度 skewness : {df[col].skew():+.2f} +0.5以上:左偏 0:正規分布 -0.5以下:右偏 ※+0.5~-0.5以内ほぼ正規分布')
print(f'尖度 kurtosis : {df[col].kurt():.2f} 2.5以下:扁平裾太 3:正規分布 3.5以上:尖り裾細 ※2.5~3.5範囲内ほぼ正規分布')
print(f'1σ : {(df[col].mean()-df[col].std()*1):.1f} ~ {(df[col].mean()+df[col].std()*1):.1f} 標準偏差±1区間')
print(f'2σ : {(df[col].mean()-df[col].std()*2):.1f} ~ {(df[col].mean()+df[col].std()*2):.1f} 標準偏差±2区間')
偏った分布の数値
-> 正規化 Normalization (Min-Max Normalization)
-> 標準化 Standardization (Z-score Normalization)
不均衡な離散値/カテゴリ値 imbalanced data
-> アンダーサンプリング Under sampling
-> オーバーサンプリング Over sampling
前処理時の判断
欠損値 missing value 参考:codexa
欠損の理由によって解決アプローチを変える
欠損値が含まれるデータセットでは学習できないアルゴリズム
線形モデル
ニューラルネットワークモデル
処理方法:そのまま扱う(欠損値の有無に意味がある場合)
穴埋めする(他の説明変数を失いたくない場合)
平均値/中央値/最頻値などで穴埋め
穴埋めする値を予測する(推論可能&高精度を求める場合)
破棄する(他の説明変数を失っても問題ない場合)
欠損値が含まれるデータセットで学習できるアルゴリズム
勾配ブースティング決定木(GBDT)モデル xgboost lightgbm catboost
処理方法:そのまま扱う(欠損値の有無に意味がある場合)
穴埋めする(他の説明変数を失いたくない場合)
平均値/中央値/最頻値などで穴埋め
穴埋めする値を予測する(推論可能&高精度を求める場合)
破棄する(他の説明変数を失っても問題ない場合)
外れ値/異常値 outliar/abnormal value 参考:BellCurve、ごちきか、GMO、東洋経済OL
探索方法:箱ひげ図を描く(データの順位を基に判定)
外れ値閾値セオリー:残差が標準偏差の2倍以上(4.6%)もしくは3倍以上(0.3%)
クラスター分析を行う
処理方法:入力ミスなどの異常値とわかるものは削除する
外れ値(異常値に見えるが異常と言いきる証拠のない数値)はむやみに削除しない
外れ値と判断した理由を明確に説明できるようにしておくこと
スケーリング
正規化 Normalization
最小値を0、最大値を1に収める Min-Max Normalization
標準化 Standardization
平均を0、標準偏差を1に収める Z-score Normalization
サンプリング
分類問題における「不均衡データ(imbalanced data)」に対し正例/負例のバランスを取る手法
アンダーサンプリング under sampling 参考:Qiita
件数が少ない方に合わせて、多い方の件数を減らす
オーバーサンプリング over sampling 参考:Qiita
件数が多い方に合わせて、少ない方の件数を増やす